如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/24 11:14:17
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC
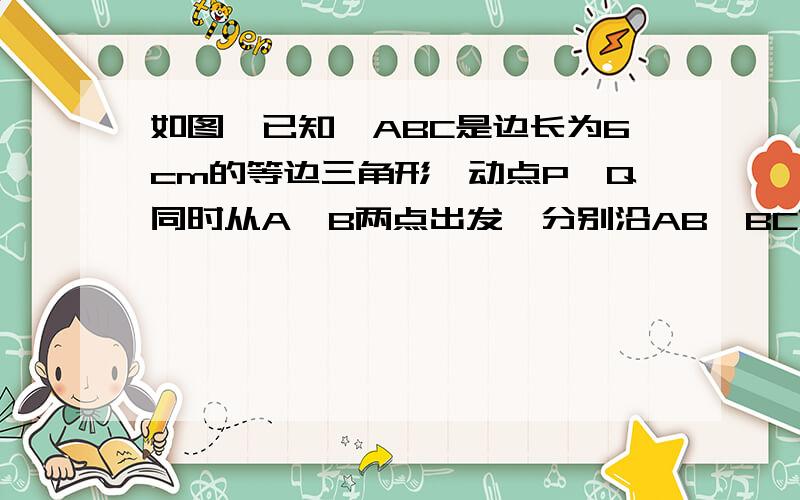
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),
(1)当t为何值时,△BPQ为直角三角形
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速
(1)BQ=2AP,要想△BPQ为直角三角形,则BP=2BQ或者BQ=2BP
先考虑BP=2BQ,此时BP=2BQ=4AP,又AP+BP=AB=6cm,因此AP=1.2cm,也就是t=1.2s;
在考虑BQ=2BP,此时BQ=2BP=2AP,又AP+BP=6cm,因此AP=3cm,刚好BQ=BC,停止运动,t=3s.
(2)△BPQ的一个底边为BP=6-t,对应的高BQ√3/2=√3t,
因此S=(6-t)× √3t/2
(3)△APR∽△PRQ,则∠PAR=∠RPQ=60度,QR∥BA,则∠QRC=∠BAC=60度
BQ=BP=2AP,AP=2cm, t=2满足△APR∽△PRQ
1)因为点P运动的速度是1cm/s,点Q运动的速度是2cm/s
即BQ=2BP,又因为△ABC是边长为6cm的等边三角形
所以,∠B=60°
假设△BPQ为直角三角形时,∠BQA=30°,则BQ=2BP
而已知BQ=2BP,所以△BPQ一直为直角三角形,t取值为大于0(秒),小于6/2=3(秒)
2)BP=t(cm),BQ=2t,又由上问可知△BPQ一直为直...
全部展开
1)因为点P运动的速度是1cm/s,点Q运动的速度是2cm/s
即BQ=2BP,又因为△ABC是边长为6cm的等边三角形
所以,∠B=60°
假设△BPQ为直角三角形时,∠BQA=30°,则BQ=2BP
而已知BQ=2BP,所以△BPQ一直为直角三角形,t取值为大于0(秒),小于6/2=3(秒)
2)BP=t(cm),BQ=2t,又由上问可知△BPQ一直为直角三角形
所以,PQ=√〔(2t)²-t²〕=t√3
S=BP·PQ/2=t·t√3/2=√3/2·t²
收起
