(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/20 07:12:49
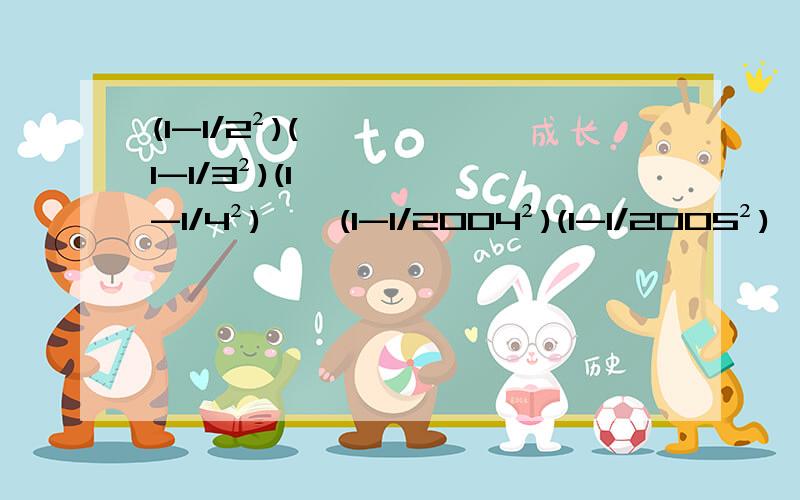
(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
原式=(1-1/2)(1+1/2)(1-1/3)(1+1/3)……(1-1/2005)(1+1/2005)
=1/2*3/2*2/3*4/3*……*2004/2005*2006/2005
=1/2*2006/2005
=1003/2005
(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
=(1+1/2)(1-1/2)(1+1/3)(1-1/3)(1+1/4)(1-1/4)...(1+1/2004)(1-1/2004)(1+1/2005)(1-1/2005)
=(3/2)(1/2)(4/3)(2/3)(5/4)(3/4)...
全部展开
(1-1/2²)(1-1/3²)(1-1/4²)……(1-1/2004²)(1-1/2005²)
=(1+1/2)(1-1/2)(1+1/3)(1-1/3)(1+1/4)(1-1/4)...(1+1/2004)(1-1/2004)(1+1/2005)(1-1/2005)
=(3/2)(1/2)(4/3)(2/3)(5/4)(3/4)...(2005/2004)(2003/2004)(2006/2005)(2004/2005)
=[(3/2)(4/3)(5/4)...(2005/2004)(2006/2005)][(1/2)(2/3)(3/4)...(2003/2004)(2004/2005)]
=[(3×4×5×...×2006)/(2×3×4×...×2005)]×[(1×2×3...×2004)/(2×3×4×...×2005)]
=(2006/2)×(1/2005)
=1003/2005
收起