已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG使点A,C分别在DG和DE上 连接AE,BG (1)试猜想线段BG和AE的数量关系(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(大于0°,
来源:学生作业帮助网 编辑:作业帮 时间:2024/12/01 12:49:28
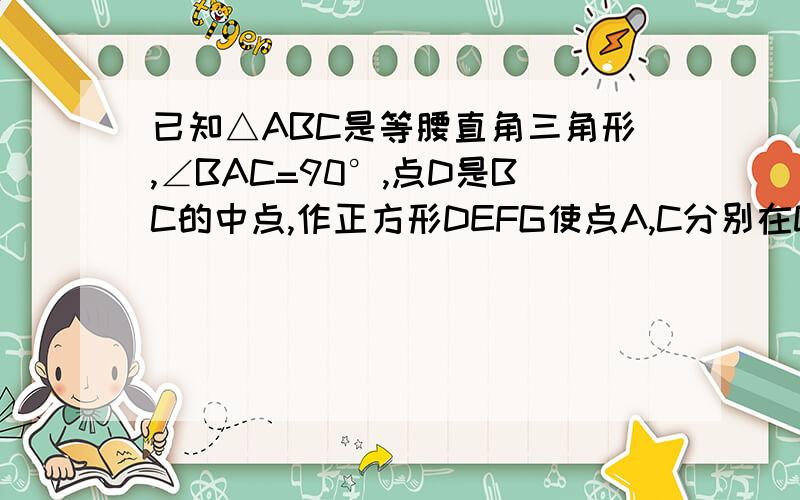
已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG使点A,C分别在DG和DE上 连接AE,BG (1)试猜想线段BG和AE的数量关系(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(大于0°,
已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG
使点A,C分别在DG和DE上 连接AE,BG (1)试猜想线段BG和AE的数量关系
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(大于0°,小于360°)判断(1)中的结论是否仍然成立?如果成立,证明;不成立说明理由
(3)若BC=DE=2,在(2)的旋转过程中,当AE为最大值时,求AF的值
已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG使点A,C分别在DG和DE上 连接AE,BG (1)试猜想线段BG和AE的数量关系(2)将正方形DEFG绕点D逆时针方向旋转一定角度后(大于0°,
(1)BG=AE
(2)将正方形DEFG绕点D逆时针方向旋转一定角度后,上述结论仍成立
证明如下:
设正方形DEFG绕点D逆时针方向旋转a度E,F,G分别转到E',F'G',DE'和AC交与,G'D和AB交于N.则,∠CDM=∠ADN=a
因为△ABC是等腰直角三角形,所以∠DCM=45°,因点D是BC的中点,
所以AD⊥BC,AD=DC=1/2BC,△ADB为等腰直角三角形,∠DAN=45°
所以△DMC≌△DNA,AN=MC,DM=DN,∠DMC=∠DNA
而AB=AC,DG'=DE',∠AME'=∠DMC,∠BNG'=∠DNA
所以AM=BN ,ME'=NG',∠AME'=∠BNG',
所以△BNG'≌△AME',BG'=AE'
(3)当E点绕D点逆时针方向旋转270°时,AE取得最大值,在RT△AE'F'中,AE=AD+DE‘=1+2=3
EF=DE=2,AF根号(AE²+EF²)=根号(9+4)=根号13
我现在才见到这道题
有人给你回答了
(1) AE=BG,
在直角三角形△ABC中,AD为斜边BC上的中线,
由等腰三角形三线合一定理和直角三角形斜边上的中线定理可知:
AD垂直平分BC,且AD=BD=DC.
在正方形DEFG中,DE= DG,
所以直角三角形BDG全等于直角三角形ADE(SAS)
所以AE=BG。
(2)逆时针旋转任意角...
全部展开
(1) AE=BG,
在直角三角形△ABC中,AD为斜边BC上的中线,
由等腰三角形三线合一定理和直角三角形斜边上的中线定理可知:
AD垂直平分BC,且AD=BD=DC.
在正方形DEFG中,DE= DG,
所以直角三角形BDG全等于直角三角形ADE(SAS)
所以AE=BG。
(2)逆时针旋转任意角度(大于0°,小于360°)后,结果依然成立。
逆时针旋转后,依然有DE= DG,AD=BD,∠BDA=∠GDE=90°
而∠BDG=∠BDA+∠ADB,∠ADE=∠GDE+∠ADB
因此,∠BDG=∠ADE
所以三角形BDG全等于三角形ADE
可知,AE=BG
(3)要使AE最大,则AE与AD共线(三角形两边之和大于第三边)
即,AE=AD+DE=3
而DE=EF=2,解直角三角形就可知,
AF=根号13。
收起