求出a,b的值,使得p=(1 -2 3)是A=(3 2 -1;a -2 2;3 b -1)的特征向量,并求出对应的特征值

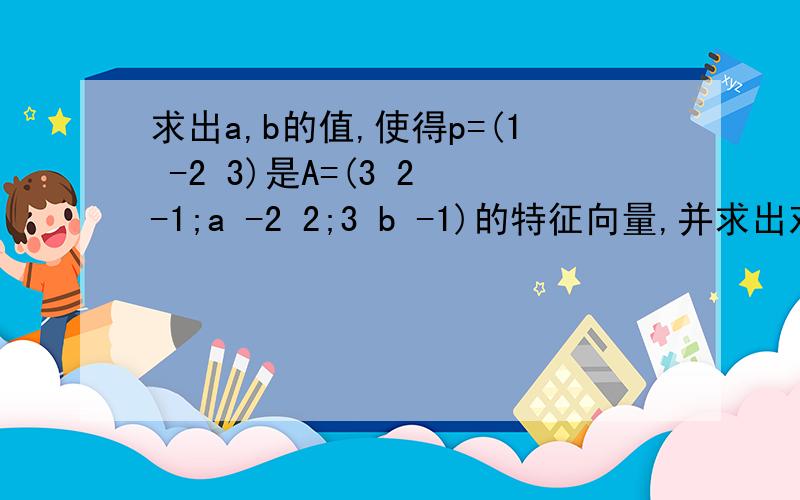
求出a,b的值,使得p=(1 -2 3)是A=(3 2 -1;a -2 2;3 b -1)的特征向量,并求出对应的特征值
求出a,b的值,使得p=(1 -2 3)是A=(3 2 -1;a -2 2;3 b -1)的特征向量,并求出对应的特征值

求出a,b的值,使得p=(1 -2 3)是A=(3 2 -1;a -2 2;3 b -1)的特征向量,并求出对应的特征值
由于Ap=λp,可知
3*1+2*(-2)+(-1)*3 = λ
a*1+(-2)*(-2)+2*3 = -2λ
3*1+b*(-2)+(-1)*3 = 3λ
解得 λ=-4,a=-2,b=6,即对应的特征值为 -4.

矩阵：
3 2 1
[ a -2 2 ]
3 b -1

λ-3 2 1
[ a λ-2 2 ] 的特征向量 p= (1, -2, 3)
3 b λ-1

...

全部展开

矩阵：
3 2 1
[ a -2 2 ]
3 b -1

λ-3 2 1
[ a λ-2 2 ] 的特征向量 p= (1, -2, 3)
3 b λ-1

(λ-3)*1 + 2*(-2) + 1*3=0
方程 { a *1+ (λ-2)*(-2) + 2*3=0
3*1 + b*(-2) + (λ-1)*3=0
得 对应特征值λ=4
a=-2
b=6

收起