菱形ABCD,对角线AC、BD交于点O、E、F、G、H分别是AB、BC、CD、DA的中点请说明E,F,G,H四个点在⊙O上
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/05 14:58:30
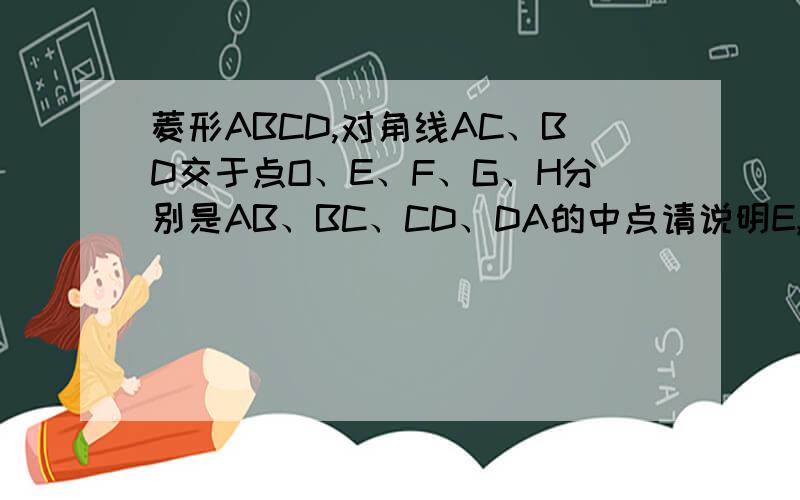
菱形ABCD,对角线AC、BD交于点O、E、F、G、H分别是AB、BC、CD、DA的中点请说明E,F,G,H四个点在⊙O上
菱形ABCD,对角线AC、BD交于点O、E、F、G、H分别是AB、BC、CD、DA的中点请说明E,F,G,H四个点在⊙O上
菱形ABCD,对角线AC、BD交于点O、E、F、G、H分别是AB、BC、CD、DA的中点请说明E,F,G,H四个点在⊙O上
说明:
菱形的对角线互相垂直平分.
所以,AC和BD相交成直角,
菱形被对角线分成四个直角三角形.
E、F、G、H分别是AB、BC、CD、DA的中点,
所以,OE,OF,OG,OH分别是四个直角三角形斜边上的中线.
直角三角形斜边上的中线等于斜边的一半.
所以,OE=AB/2,OF=BC/2,OG=CD/2,OH=DA/2.
菱形ABCD中,AB=BC=CD=DA.
所以,OE=OF=OG=OH,
根据到定点的距离等于定长的点在同一圆上,
所以,E,F,G,H四个点在⊙O上
然后呢,题都不写完.
这个“⊙O”是指什么意思???
只要证O点到E、F、G、H距离相等即可
对三角形OEB和三角形OFB,,角OBA=角OBC,(菱形对角线平分角),OB=OB,EB=(1/2)*AB=(1/2)*BC=BF,由边角边可知三角形OEB和三角形OFB为全等,故有OE=OF,同理有OF=OG,OG=OH,
所以可得O点到E、F、G、H距离相等,即都在一个圆上
连结EF.FG.GH.HE
因为E、H分别是AB、DA的中点
所以EH为BD的中位线
所以EH//BD
同理FG//BD,EF//HG//AC
所以四边形EFHG为平行四边形
又因为菱形ABCD中AC垂直于BD,且EH//BD,HG//AC
所以EH//HG
所以平行四边形EFHG为矩形
所以EG=FH
又OF=OH=...
全部展开
连结EF.FG.GH.HE
因为E、H分别是AB、DA的中点
所以EH为BD的中位线
所以EH//BD
同理FG//BD,EF//HG//AC
所以四边形EFHG为平行四边形
又因为菱形ABCD中AC垂直于BD,且EH//BD,HG//AC
所以EH//HG
所以平行四边形EFHG为矩形
所以EG=FH
又OF=OH=1/2FH,OE=OG=1/2EG
所以OE=OF=OG=OH
即E、F、G、H是在以O为圆心,以OE(或OF.OH.OG)为半径的圆上
收起
5 drsert5gvbewa54tg