(1)如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=Ce,求∠EBD。(2)如图,某船在上午11点30分在A处观测岛B在东偏北30°,该船以10海里、时的速度向东航行到C处,在观测海岛在东偏
来源:学生作业帮助网 编辑:作业帮 时间:2024/12/01 09:12:03
(1)如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=Ce,求∠EBD。(2)如图,某船在上午11点30分在A处观测岛B在东偏北30°,该船以10海里、时的速度向东航行到C处,在观测海岛在东偏
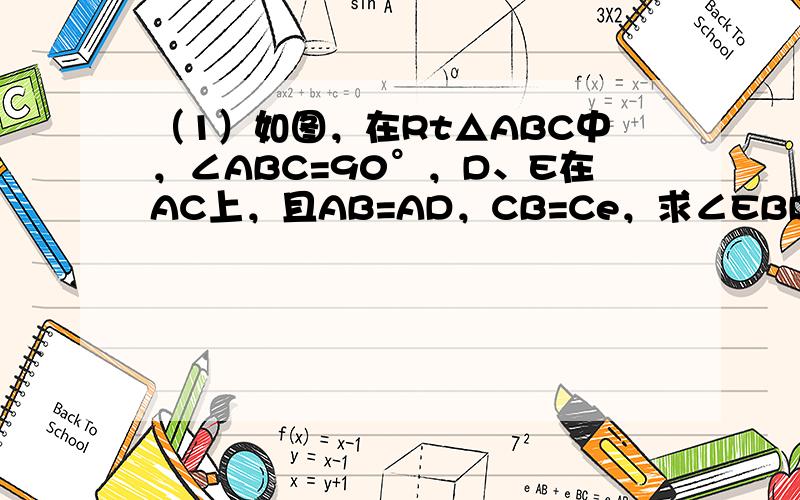
(1)如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=Ce,求∠EBD。
(2)如图,某船在上午11点30分在A处观测岛B在东偏北30°,该船以10海里、时的速度向东航行到C处,在观测海岛在东偏北60°,且船距海岛40公里。(不得用勾股定理)
①求船到C点的时间
②若该船从C点继续向东航行,何时到达B岛正南处的D处?
(1)如图,在Rt△ABC中,∠ABC=90°,D、E在AC上,且AB=AD,CB=Ce,求∠EBD。(2)如图,某船在上午11点30分在A处观测岛B在东偏北30°,该船以10海里、时的速度向东航行到C处,在观测海岛在东偏
(1)因为AB=AD CB=CE
所以∠ABD=∠ADB ∠CBE=∠CEB
∠ABD+∠CBE=(180°-∠A)/2+(180°-∠C)/2
=[360°-(∠A+∠C)]/2
因为∠ABC=90°
所以∠A+∠C=180°-∠ABC=180°-90°=90°
所以∠ABD+∠CBE=(360°-90°)/2
=135°
所以∠EBD=135°-90°=45°
(2)①因为船在A处观测岛B在东偏北30° 所以∠ACB=180°-60°=120° ∠A=30°
所以∠ABC=180°-120°-30°=30°
所以∠A=∠ABC
所以AC=BC
因为船在C处距海岛40公里 该船以10海里
所以AC=40 40/10=4
船到C点的时间是15点30分
②因为BD⊥CD 航行到C处在观测海岛在东偏北60°
所以∠BCD=90° ∠BCD=60°
∠CBD=180°-90°-60°=30°
因为直角三角形中有一个锐角等于30°,
所以CD=1/2BC
因为BC=40
所以CD=20
20/10=2
随意17点30分船到达B岛正南处的D处
第一题
在△BEC中
∵CB=CE
∴∠CBE=∠CEB
∴∠CEB=(180°-∠C)/2
同理可得
∠BDE=(180°-∠A)/2
∠EBD=180°-∠BDE-∠CEB
∴∠EBD=180°-(180°-∠C)/2-(180°-∠A)/2
整理得∠EBD=(∠A+∠C)/2
∠A+∠C=90°
∴∠EB...
全部展开
第一题
在△BEC中
∵CB=CE
∴∠CBE=∠CEB
∴∠CEB=(180°-∠C)/2
同理可得
∠BDE=(180°-∠A)/2
∠EBD=180°-∠BDE-∠CEB
∴∠EBD=180°-(180°-∠C)/2-(180°-∠A)/2
整理得∠EBD=(∠A+∠C)/2
∠A+∠C=90°
∴∠EBD=90°/2=45°
第二题
过点B作BD⊥AC交AC延长线与点D
由题意可得∠BAD=30°,∠BCD=60°,∴∠CBD=30°
由直角三角形斜边中线等于斜边一半可求出
CD=20海里
剩下的就好做了,不说了
希望对您有帮助
收起
(1)为30度
1)45度
2)下午3点30分到C
到D点是5点30分