基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√

来源：学生作业帮助网 编辑：作业帮 时间：2024/11/24 18:53:23
基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√
xTnX~ԫD ,.I^D!bBʶ1$&6`x>C{ؾ+;>.-{{Zi%3͜w̮zV祡Ƶ4btTmmr]-է+zOUf4ZȸWD4b(83Pjg5j;AZbm 12QFTCŹW^CL A~sB7]-t f忍v(vfA{r\a\fRGGu+ZsYR|XÜtO0K:hhbΟ Tb`/Tqu̶L6/ͭUv 7Rcm9q'  ,aQrz0E?a.d[k(]sD+n_qD.@%9]tYWqí `}ey y3LS洃m-3Dok­eV-FiQp%JvV)I)[XA97dk9HΔE%{mn[qEǟK<$#\q-aتKVbl̤^F+ 7lᤶ'F:?/oq&eU:ވfx`k<8)?~n\z^Z+#[O 7B ZՏy]2,X%U<HK5ĵrxZ"qHC]g^S>R0Q_wJ=0H7އ2o?C2 bY0tmZ >+(H

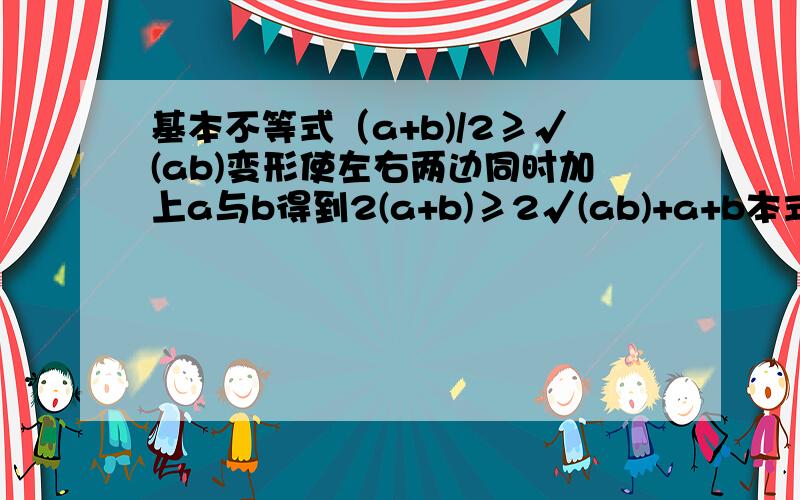
基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√
基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4
（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√b)^2 /4这里√(ab)与(√a+√b)^2 /4的关系是什么,为什么不等式同一式子变形后会出现不同变化

基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√
假定a和b都有是按公式定义的,你所推导出的式子在本质上与基本公式一致,只不过你中间加了一步：(a+b)/2=(a+b)/4+(a+b)/4 ≥ (a+b)/4+√(ab)/2=(√a+√b)^2 /4,这中间有一处使用了不等号就是就用基本公式得来的.
基本公式的变形在很多时候还很有用的,三角函数中倍角的余弦公式、梯形的面积等于两底和之半乘高除以2与其中线长度乘2、圆的面积лr^2与лd^2/4、余弦定理中的求边与求角公式等.即便如本问中的不等式,也分作调和平均数、几何平均数、算术平均数和均方根若干比较式,它们导出都依存于基本公式.

如果a、b都是负数呢？我的朋友，ab可以是正的，因为a、b可以是全正的或者是全负的，但是不能分开的。明白？ √(ab) 这个可以有，但 √a和√b不可以有，你无形中约定了a、b都是正数，明白？呵呵。

a^2+b^2>=2ab,(a+b)^2>=4ab,((a+b)/2)^2>=ab,换元可得√(ab)<=(√a+√b)^2 /4,a=b时，"="成立为神马不等式同一式子变形后会出现不同变化，是不是我变形中有问题不是，因为（a+b)/2≥√(ab)和(a+b)/2≥(√a+√b)^2 /4两式取等号的条件是相同的，都是a=b,而此时√(ab)=(√a+√b)^2 /4，所以两式确定范围还是相同的...

全部展开

a^2+b^2>=2ab,(a+b)^2>=4ab,((a+b)/2)^2>=ab,换元可得√(ab)<=(√a+√b)^2 /4,a=b时，"="成立

收起

一个数大于等于零,能用不等式基本性质2吗高一不等式基本性质2 a+b≥2√ab 基本不等式（a+b)/2≥√(ab)变形使左右两边同时加上a与b得到2(a+b)≥2√(ab)+a+b本式右边得(√a+√b)^2 后使左右两边同时除4得到(a+b)/2≥(√a+√b)^2 /4（a+b)/2≥√(ab)这式子变形会出现(a+b)/2≥(√a+√ 求道高一基本不等式题目.已知a＞b,ab=1,证明：a²+b²≥2√2（a-b）.【利用基本不等式】 基本不等式,a+b≥2根号下ab,为什么a,b不能等于0呢 基本不等式a^2+b^2≥2ab 变形 ab≤((a+b)/2)^2 与a^2+b^2≥((a+b)^2)/2 是如何得到的?这三个式子a b的范主要是这三个式子a b所要符合的条件? 基本不等式问题设a,b,c都是正数 求证:a+(1/b),b+(1/c),c+(1/a)三个数中至少有一个不小于2请用基本不等式[(a+b)/2≥√ab]解答 证明a(a-b)≥b(a-b),要用基本不等式 根号ab≥a+b/2 的那个 高中数学基本不等式a+b>=2√ab证明如题 证明a+b>=2√ab成立 一道基本不等式题目2/(1/a+1/b)与√ab的大小 1.已知一个直角三角形三边之和是2,求这个直角三角形面积最大值.利用基本不等式求解】2.已知a＞b,ab=1,证明：a²+b²≥2√2（a-b）.【利用基本不等式】 柯西不等式推导基本不等式这么推导?我说的是证明(a+b)大于等于2√ab 关于基本不等式的一些基本问题.1.有个式子是(a+b)/2≥√(a+b).为什么当且仅当a=b时等号成立,而不是 √a=√b呢?2.为什么基本不等式没有a^2+b^2≥-2ab,只有a^2+b^2≥2ab?做题目的时候老想用第一个公 基本不等式变形 关于高中基本不等式若正数A,B满足AB=A+B+3,则AB的取值范围是：AB=A+B+3≥2√AB+3AB-2√AB-3≥0(√AB-3)(√AB+1)≥0(√AB)≥3AB)≥9(当且仅当A＝B时取等号）以上没有问题疑惑：利用基本不等式 ab=0ab>=9或ab 用分析法证明基本不等式a+b/2>=√ab如题(a>0,b>0) 关于数学的基本不等式：知a>0,b>0,则1/a+1/b+2√ab的最小值 基本不等式的变形中,a＋b小于什么注意是小于 基本不等式解答比较a^2 + b^2 + ab + 1与a + b的大小.