Sn=1*2+2*3+3*4+4*5+5*6+……+n*(n+1)=?
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/06 08:02:02
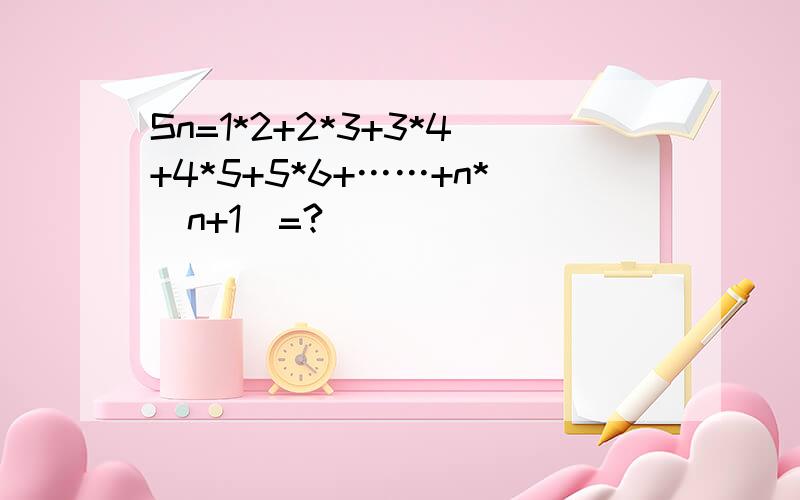
Sn=1*2+2*3+3*4+4*5+5*6+……+n*(n+1)=?
Sn=1*2+2*3+3*4+4*5+5*6+……+n*(n+1)=?
Sn=1*2+2*3+3*4+4*5+5*6+……+n*(n+1)=?
分成1+2+3+……+n+(1^2+2^2+3^2+……+n^2)=(1+n)*n/2+1/6*n(n+1)(2n+1)=(n+1)*(n+2)*n/3.
重点是怎么求1^2+2^2+……+n^2,这里讲2种方法,设Sn=1^2+2^2+……+n^2.
方法1:
展开成1+2+3+4+5……+n
+2+3+4+5+……+n
3+4+5+……+n
4+5+……+n
……
+n
用求和公式:
(1+n)n/2
+(2+n)(n-1)/2
+……
+(n+n)(n-(n-1))/2
化简=0.5*[(n+1)n+(n+2)(n-1)+(n+3)(n-2)+(n+4)(n-3)+……(n+n)(n-(n-1)]=0.5*[n^2*n+n*n-(2^2+……+n^2)+(2+3+4+……+n)]=0.5*[n^3+n^2-(Sn-1)+(n+2)(n-1)/2]
这就相当于得到一个关于Sn的方程.
化简一下:
n^3+n^2+1+(n+2)(n-1)/2=3Sn,得
Sn=1/3*n^3+1/2*n+1/6*n即
1/6*n(n+1)(2n+1)
方法2:
Sn=S(n-1)+n^2
=S(n-1)+1/3*[n^3-(n-1)^3]+n-1/3
=S(n-1)+1/3*[n^3-(n-1)^3]+1/2*[n^2-(n-1)^2]+1/6
=S(n-1)+1/3*[n^3-(n-1)^3]+1/2*[n^2-(n-1)^2]+1/6*[n-(n-1)]
即Sn-1/3*n^3-1/2*n^2-n/6=S(n-1)-1/3*(n-1)^3-1/2*(n-1)^2-(n-1)/6
好了!等式左面全是n,右面全是(n-1),以此递推下去,得
Sn-1/3*n^3-1/2*n^2-n/6
=S(n-1)-1/3*(n-1)^3-1/2*(n-1)^2-(n-1)/6
=S(n-2)-1/3*(n-2)^3-1/2*(n-2)^2-(n-2)/6
……
=S(1)-1/3*(1-1)^3-1/2*(1-1)^2-(1-1)/6
=0
所以Sn=1/3*n^3+1/2*n+1/6*n
通常我们是当成一个等式背下来,再带到要求的数列中去.
an=n(n+1)=n²+n
Sn=(1+2+……+n)+(1²+2²+……+n²)
=n(n+1)/2+n(n+1)(2n+1)/6
=n(n+1)n+2)/3