证2/1*4/3*6/5*8/7*.(2n)/(2n-1)>√(2n+1)
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/17 08:53:06
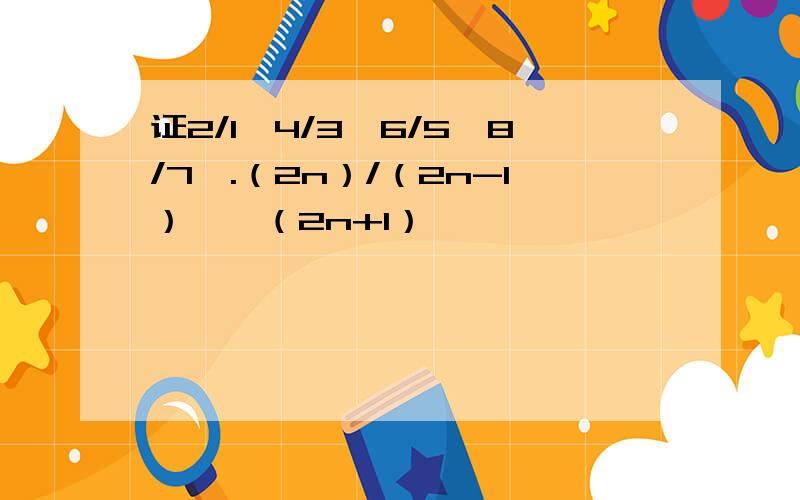
证2/1*4/3*6/5*8/7*.(2n)/(2n-1)>√(2n+1)
证2/1*4/3*6/5*8/7*.(2n)/(2n-1)>√(2n+1)
证2/1*4/3*6/5*8/7*.(2n)/(2n-1)>√(2n+1)
2^2 > 1*3
4^2 > 3*5
.
(2n)^2 > (2n-1)(2n+1)
∴(2*4*6*8*...2n)^2 > 1*3^2*5^2*7^2*...(2n-1)^2*(2n+1)
∴[(2*4*6*8*...2n)/(1*3*5*7*...(2n-1))]^2 > 2n+1
∴2/1*4/3*6/5*8/7*.(2n)/(2n-1) > √(2n+1)
利用数学归纳法
(1)当n=1时,不等式左边:2/1=2,不等式右边:√(2+1)=√3,左边>右边成立;
(2)假设n=k时,2/1*4/3*6/5*......(2k)/(2k-1)>√(2k+1)成立
(3)那么n=k+1时,不等式左边:2/1*4/3*6/5*......(2k)/(2k-1)*[2(k+1)]/[2(k+1...
全部展开
利用数学归纳法
(1)当n=1时,不等式左边:2/1=2,不等式右边:√(2+1)=√3,左边>右边成立;
(2)假设n=k时,2/1*4/3*6/5*......(2k)/(2k-1)>√(2k+1)成立
(3)那么n=k+1时,不等式左边:2/1*4/3*6/5*......(2k)/(2k-1)*[2(k+1)]/[2(k+1)-1]> [√(2k+1)]*[2(k+1)]/[2(k+1)-1];
[√(2k+1)]*[2(k+1)]/[2(k+1)-1]=√[(2k+2)(2k+2)/(2k+1)]
又(2k+2)(2k+2)=4k∧2+8k+4>4k∧2+8k+3=(2k+1)(2k+3);
所以(2k+2)(2k+2)/(2k+1)>(2k+3)=2(k+1)+1,有[√(2k+1)]*[2(k+1)]/[2(k+1)-1]>√[2(k+1)+1]成立;
即n=k+1时,不等式成立
得证。
收起