如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= 23．设直线AC与直线x=4交于点E．（1）求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；（2）设（

来源：学生作业帮助网 编辑：作业帮 时间：2024/11/16 14:58:30
如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= 23．设直线AC与直线x=4交于点E．（1）求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；（2）设（
xVKSV+:&-K-73lv6ddבĴu!:M.&B$$@@ذ?q}e/H(4]d3Y йwst+8]=ۏ_S=bD+Nǫ"8ч$-MoJ^tZ/8ȶ,F "i}zЮF2bXU &͔*'JHQ̡PFIfO:rb]+W g F l4K &3,F$G( {'O{sU#GH" ("_3[REh1:og֣yhsrTxȗfyn`s7sAE6؏dIFKXk8 Y"|ђp$>%%6Ny%*uyȪC>j|p9t3\jOb]2ۋx2jů6KѪm2ϟyqu p/ns ȉ>"]@x}x9O/wW.<Ј^ ކحn ߪDhqJx1DR Pk磎t_A} X)5SZtƃ YK`ݏ&MnƿG8l% 7k.ĤS08ID\vfi=FzfaOsz2z4A.\  "z\#=AXƓzz QtPq-d+nmԺA"z?AQ[ޯ~/*d&< *O~ܦ{^rĈU{)jUʝ]b*<9Fγ0G̈й74D0ltbN[ﴸ9F ZZ3/a#

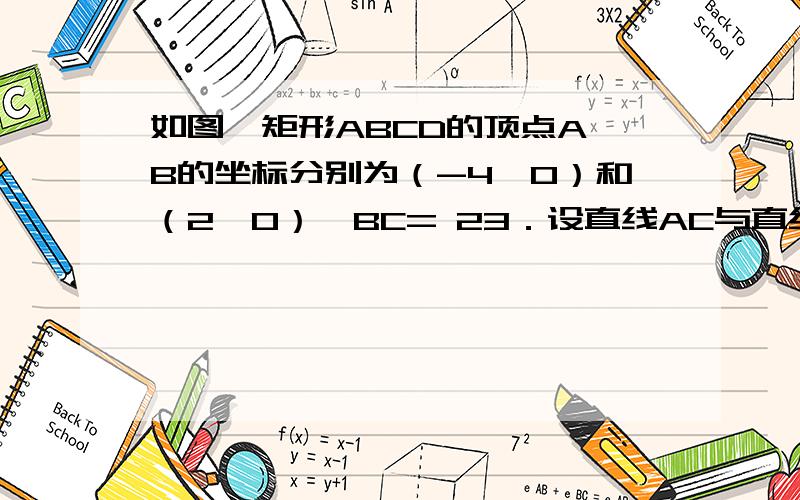
如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= 23．设直线AC与直线x=4交于点E．（1）求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；（2）设（
如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= 23．设直线AC与直线x=4交于点E．
（1）求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；
（2）设（1）中的抛物线与x轴的另一个交点为N,M是该抛物线上位于C、N之间的一动点,求△CMN面积的最大值

如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= 23．设直线AC与直线x=4交于点E．（1）求以直线x=4为对称轴,且过C与原点O的抛物线的函数关系式,并说明此抛物线一定过点E；（2）设（
（1）如图；易知：△ABC∽△AFE；
∴ CBEF=ABAF；
由题意知：AF=8,AB=6,BC=2 3；
∴EF= 833,
即E（4,833）；
设抛物线的解析式为：y=a（x-4）2+h（a≠0）,由于抛物线经过C（2,2 3）,O（0,0）；
则有：{16a+h=04a+h=23,
解得 {a=-36h=833；
∴抛物线的解析式为y=- 36（x-4）2+ 833=- 36x2+ 433x；
其顶点坐标为（4,833）,正好与E点坐标相同,故此抛物线一定经过E点；
（2）过M作MQ∥y轴,交x轴于Q,交直线CN于P；
易知：N（8,0）,C（2,2 3）；
可得直线CN的解析式为y=- 33x+ 833；
设点Q的坐标为（m,0）,则P（m,- 33m+ 833）,M（m,- 36m2+ 433m）；
∴MP=- 36m2+ 433m-（- 33m+ 833）=- 36m2+ 533m- 833；
∴S=S△CMN= 1/2MP•|XN-XC|= 12×（- 36m2+ 533m- 833）×6=- 32m2+5 3m-8 3；
即S=- 32（m-5）2+ 932（2＜m＜8）；
∵2＜5＜8,
∴当m=5时,Smax= 932；
即△CMN的最大面积为 932．
连BM即可．

解；因为 CM垂直于BD 所以 ∠E=90—∠ MNE因为 ∠NAD+∠ADN=∠ MNE因为 矩形ABCD所以 ∠BAD=90因为 AN平分∠BAD所以 ∠NAD=45所以 ∠CAE=45-∠DAC，∠MNE=45+∠ADB所以 ∠E=90-（45+∠ADB）在矩形ABCD中AC=BO，AO=1/2AC，DO=1/2BD 所以 OA=OD所以 ∠DAC=∠ADB因...

全部展开

解；因为 CM垂直于BD 所以 ∠E=90—∠ MNE因为 ∠NAD+∠ADN=∠ MNE因为 矩形ABCD所以 ∠BAD=90因为 AN平分∠BAD所以 ∠NAD=45所以 ∠CAE=45-∠DAC，∠MNE=45+∠ADB所以 ∠E=90-（45+∠ADB）在矩形ABCD中AC=BO，AO=1/2AC，DO=1/2BD 所以 OA=OD所以 ∠DAC=∠ADB因为 ∠E=∠CAE所以：AC=CE是等腰三角形因为EC平行于BD，所以 角DBC=角ECB又因为CB垂直于AE，所以角ABC=角EBC=90度再加条公共边BC,根据角边角定理三角形ACB全即是三角形ECB所以AC=EC所以三角形ACE为等腰三角形

收起

如图,在一个平面直角坐标系中,矩形ABCD的顶点O在坐标原点,顶点B坐标为(6,2√3 ),顶点A,C...如图,在一个平面直角坐标系中,矩形ABCD的顶点O在坐标原点,顶点B坐标为(6,2√3 ),顶点A,C分别在x轴和y轴 如图,矩形ABCD的顶点A坐标为(0,0),顶点B的坐标是(-2,1),顶点C在y轴上. 如图,矩形ABCD的顶点A坐标为（0,0）,顶点B的坐标是（-2,1）,顶点C在y轴上． 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为（1,0）,对角线的交点P的坐标为（2分之5,1）（1）分别写出顶点B,C,D的坐标;(2) 若在AB上有一点E(二分之三,0),经过点E的直线L能否将矩形ABCD分为面 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为（1,0）对角线的交点P的坐标为(二分之五,1）1 分别求出顶点B,C,D的坐标2 若在AB上有一点E(二分之三,0),经过点E的直线L能否将矩形ABCD分为面积相等 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为（1,0）,对角线的交点P的坐标为（二分之五,1）.1）.分别写出顶点B,C,D的坐标?（2）.若在AB上有一点E（二分之三,0）,经过点E的直线l能否将矩形ABCD 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为（1,0）对角线的交点P的坐标为(二分之五,1）1 分别求出顶点B,C,D的坐标2 若在AB上有一点E(二分之三,0),经过点E的直线L能否将矩形ABCD分为面积相等 【急,现等】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为（-8,4）．过 如图,在直角坐标系中,矩形ABCD的顶点A的坐标为（1,0）.对角线的交点p的坐标为（3,-3/2）一 分别写出B,C,D的坐标二 若AB上有一点E（3/2,0）,经过点E的直线L能否将矩形ABCD分成面积相等的两部分? 如图,矩形ABCD的顶点A、B的坐标分别为（-4,0）和（2,0）,BC= ．设直线AC与直线x=4交于点E． （1）求以 如图,菱形ABCD的对角线长分别为a,b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然如图,菱形ABCD的对角线长分别为a、b,以菱形ABCD各边的中点为顶点作矩形A1B1C1D1,然后再以矩形A1B1C1D1的中点为定点 如图,二次函数y=-mx^2+4m的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上.如图,二次函数y=-mx^2+4m的顶点坐标为(0,2),矩形ABCD的顶点B,C在x轴上,A ,D再跑无线上,矩形ABCD在抛物线与x轴所围成的图形内.（1） 如图7,在平面直角坐标系中,矩形OABC的顶点O与坐标原点重合如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为（4,2）．过点D（0,3）和E（6,0）的直线 如图四边形ABCD各顶点的坐标分别为A(-2,3)B(-3,1)C(1,-2)D(2,2)求四边形ABCD的面积 如图,矩形OABC的顶点坐标分别为原点O、A点(10,0),B点(10,6),C点(0,6),过点D 已知矩形ABCD在平面直角标系中,顶点A,D的坐标分别为A(0,0),图,已知矩形ABCD在平面直角标系中,顶点A、D的坐标分别为A（0,0）、D（0,4）,顶点B在x轴上,且AB=│m│(m≠0)写出B、C两点的坐标,并在图中 在直角坐标系中,矩形ABCD的顶点坐标为A(-4,0),B(0,0),C(0,2),D(-4,2).将矩形的边AB和BC的长分别扩大一倍,得到一个新的矩形,B点不动,所得新的矩形的四个顶点坐标分别是什么?若A点不动呢? 请问2014年云南省中考数学试卷23题要如何做才好呢?这题算是中考压轴题吧.已知如图平面直角坐标系中,点O是坐标原点,矩形ABCD是顶点坐标分别为A(3,0),B(3,4),C(0,4).点D在y轴上,且点D的坐标为(0,-5)