еҰӮеӣҫ,в–іABCе’Ңв–іCDEйғҪжҳҜзӯүиҫ№дёүиҫ№еҪў,B,C,DеңЁдёҖжқЎзӣҙзәҝдёҠ,иҝһз»“BEдёҺADеҲҶеҲ«дёҺAC,CEдәӨдәҺзӮ№F,G,иҜ•иҜҙжҳҺдёӢеҲ—з»“и®әжҲҗз«Ӣзҡ„зҗҶз”ұ:пјҲ1пјүAD=BEпјҲ2пјүв–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪўпјҲ3пјүиӢҘM,NеҲҶеҲ«жҳҜBE,ADзҡ„дёӯзӮ№,иҜ•иҜҙжҳҺ:в–іCMNжҳҜзӯүиҫ№
жқҘжәҗпјҡеӯҰз”ҹдҪңдёҡеё®еҠ©зҪ‘ зј–иҫ‘пјҡдҪңдёҡеё® ж—¶й—ҙпјҡ2024/11/02 16:30:45
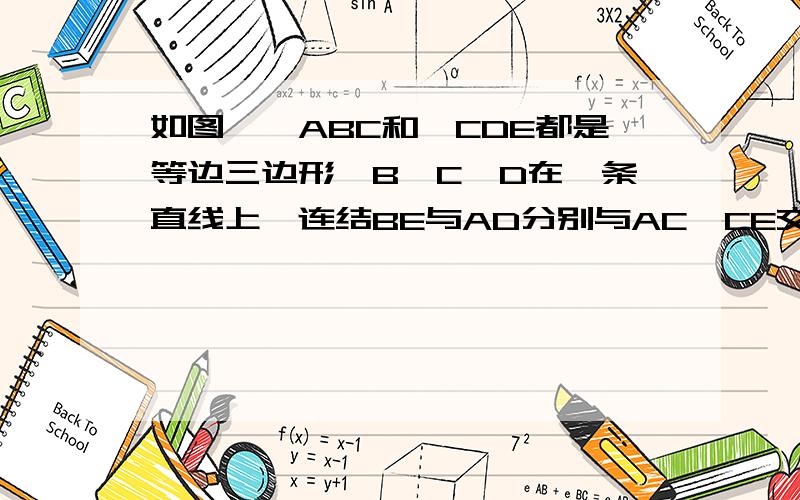
еҰӮеӣҫ,в–іABCе’Ңв–іCDEйғҪжҳҜзӯүиҫ№дёүиҫ№еҪў,B,C,DеңЁдёҖжқЎзӣҙзәҝдёҠ,иҝһз»“BEдёҺADеҲҶеҲ«дёҺAC,CEдәӨдәҺзӮ№F,G,иҜ•иҜҙжҳҺдёӢеҲ—з»“и®әжҲҗз«Ӣзҡ„зҗҶз”ұ:пјҲ1пјүAD=BEпјҲ2пјүв–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪўпјҲ3пјүиӢҘM,NеҲҶеҲ«жҳҜBE,ADзҡ„дёӯзӮ№,иҜ•иҜҙжҳҺ:в–іCMNжҳҜзӯүиҫ№
еҰӮеӣҫ,в–іABCе’Ңв–іCDEйғҪжҳҜзӯүиҫ№дёүиҫ№еҪў,B,C,DеңЁдёҖжқЎзӣҙзәҝдёҠ,иҝһз»“BEдёҺADеҲҶеҲ«дёҺAC,CEдәӨдәҺзӮ№F,G,иҜ•иҜҙжҳҺдёӢеҲ—з»“и®әжҲҗз«Ӣзҡ„зҗҶз”ұ:
пјҲ1пјүAD=BE
пјҲ2пјүв–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪў
пјҲ3пјүиӢҘM,NеҲҶеҲ«жҳҜBE,ADзҡ„дёӯзӮ№,иҜ•иҜҙжҳҺ:в–іCMNжҳҜзӯүиҫ№дёүи§’еҪў.
еӣҫеҫҲжҪҰиҚү.
еҰӮеӣҫ,в–іABCе’Ңв–іCDEйғҪжҳҜзӯүиҫ№дёүиҫ№еҪў,B,C,DеңЁдёҖжқЎзӣҙзәҝдёҠ,иҝһз»“BEдёҺADеҲҶеҲ«дёҺAC,CEдәӨдәҺзӮ№F,G,иҜ•иҜҙжҳҺдёӢеҲ—з»“и®әжҲҗз«Ӣзҡ„зҗҶз”ұ:пјҲ1пјүAD=BEпјҲ2пјүв–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪўпјҲ3пјүиӢҘM,NеҲҶеҲ«жҳҜBE,ADзҡ„дёӯзӮ№,иҜ•иҜҙжҳҺ:в–іCMNжҳҜзӯүиҫ№
пјҲ1пјүвҲөв–іABCе’Ңв–іCDEдёәзӯүиҫ№дёүи§’еҪў
вҲҙAC=BC CD=CE вҲ ACB=вҲ DCE=60еәҰ
вҲөвҲ BCE=вҲ ACE+вҲ ACB
вҲ ACD=вҲ ACE+вҲ DCE
вҲҙвҲ BCE=вҲ ACD
еңЁв–іBCEе’Ңв–іACDдёӯ
AC=BC CD=CE вҲ BCE=вҲ ACD
вҲҙв–іBCEвүҢв–іACDпјҲSASпјү
вҲҙAD=BE
пјҲ2пјүвҲөв–іACDвүҢв–іBCE
вҲҙвҲ CAG=вҲ CBE
еңЁв–іCBFдёҺв–іCAGдёӯ
вҲөвҲ BCF=вҲ ACG=60еәҰ вҲ CBF=вҲ CAG AC=BC
вҲҙв–іCBFвүҢв–іCAG
вҲҙCF=CG
вҲөвҲ FCG=60еәҰ
вҲҙв–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪў
пјҲ3пјүвҲөCMжҳҜв–іBCEдёӯBEиҫ№дёҠзҡ„дёӯзәҝ,CNжҳҜв–іACDдёӯADиҫ№дёҠзҡ„дёӯзәҝ
вҲҙ CM=CN
еҲҷ AN=1/2 AD=1/2 BE=BM NC=MC AC=BC
вҲҙв–іANCвүҢв–іBMC
вҲҙ вҲ ACN=вҲ BCM
еҲҷвҲ MCN=вҲ ACM+вҲ ACN=вҲ ACM+вҲ BCM=вҲ ACB=60еәҰ
вҲҙв–іCMNжҳҜзӯүиҫ№дёүи§’еҪў
иҜҒжҳҺпјҡ
(1)з”ұдәҺвҲ ACB=вҲ ECD=60пјҢж•…вҲ ACD=вҲ BCEпјҢеҸҲAC=BCпјҢCD=CEпјҢж•…жңүв–іACDвүҢв–іBCEпјҢж•…AD=CE
(2)з”ұBCDе…ұзәҝжңүвҲ ACE=60
з”ұ(1)жңүвҲ FBC=вҲ GACпјҢеҸҲвҲ FCB=вҲ GCA=60пјҢBC=ACпјҢж•…жңүв–іFBCвүҢв–іGACпјҢж•…CF=CGпјҢеҲҷв–іCFGзӯүиҫ№
(3)з”ұ(1)жңүCM=CNпјҢдё”вҲ MCE=вҲ NCD
ж•…вҲ MCN=вҲ MCD...
е…ЁйғЁеұ•ејҖ
иҜҒжҳҺпјҡ
(1)з”ұдәҺвҲ ACB=вҲ ECD=60пјҢж•…вҲ ACD=вҲ BCEпјҢеҸҲAC=BCпјҢCD=CEпјҢж•…жңүв–іACDвүҢв–іBCEпјҢж•…AD=CE
(2)з”ұBCDе…ұзәҝжңүвҲ ACE=60
з”ұ(1)жңүвҲ FBC=вҲ GACпјҢеҸҲвҲ FCB=вҲ GCA=60пјҢBC=ACпјҢж•…жңүв–іFBCвүҢв–іGACпјҢж•…CF=CGпјҢеҲҷв–іCFGзӯүиҫ№
(3)з”ұ(1)жңүCM=CNпјҢдё”вҲ MCE=вҲ NCD
ж•…вҲ MCN=вҲ MCD-вҲ NCD=вҲ MCD-вҲ MCF-вҲ FCE=вҲ MCD-вҲ MCF-вҲ ECD=вҲ FCE=60
ж•…в–іCMNзӯүиҫ№
иҜҒжҜ•
收иө·
пјҲ1пјүвҲөв–іABCе’Ңв–іCDEдёәзӯүиҫ№дёүи§’еҪў
вҲҙAC=BC CD=CE вҲ ACB=вҲ DCE=60еәҰ
еҸҲвҲөвҲ BCE=вҲ ACE+вҲ ACB
вҲ ACD=вҲ ACE+вҲ DCE
вҲҙвҲ BCE=вҲ ACD
еңЁв–іBCEе’Ңв–іACDдёӯ
AC=BC CD=CE вҲ BCE=вҲ ACD
вҲҙв–іBCEвүҢв–іACDпјҲSASпјү
вҲҙAD=BE
иҜҒжҳҺпјҡ
(1)
вҲөAC=BCпјҢCE=CDпјҢвҲ ACD=вҲ BCE=120В°
вҲҙв–іACDвүҢв–іBCEгҖҗSASгҖ‘
вҲҙAD=BE
(2)
вҲөв–іACDвүҢв–іBCE
вҲҙвҲ BEC=вҲ ADC
еҸҲвҲөвҲ ECD=вҲ FCE=60В° CE=CD
вҲҙв–іFCEвүҢв–іGCDгҖҗASAгҖ‘
вҲҙCF=CG дё”вҲ ACE=60В°
вҲҙв–іFCGжҳҜзӯүиҫ№дёүи§’еҪў
...
е…ЁйғЁеұ•ејҖ
иҜҒжҳҺпјҡ
(1)
вҲөAC=BCпјҢCE=CDпјҢвҲ ACD=вҲ BCE=120В°
вҲҙв–іACDвүҢв–іBCEгҖҗSASгҖ‘
вҲҙAD=BE
(2)
вҲөв–іACDвүҢв–іBCE
вҲҙвҲ BEC=вҲ ADC
еҸҲвҲөвҲ ECD=вҲ FCE=60В° CE=CD
вҲҙв–іFCEвүҢв–іGCDгҖҗASAгҖ‘
вҲҙCF=CG дё”вҲ ACE=60В°
вҲҙв–іFCGжҳҜзӯүиҫ№дёүи§’еҪў
(3)
вҲөAD=BE
вҲҙBM=BE/2=AD/2=AN
еҸҲвҲөв–іACDвүҢв–іBCE
вҲҙвҲ CAD=вҲ CBE
вҲөAC=BC
вҲҙв–іACNвүҢв–іBCMгҖҗSASгҖ‘
вҲҙCM=CNпјҢвҲ BCM=вҲ ACN
вҲөвҲ MCN=вҲ BCN-вҲ BCM=вҲ BCN-вҲ ACN=вҲ ACB=60В°
вҲҙв–іCMNжҳҜзӯүиҫ№дёүи§’еҪў
иҜҒжҜ•пјҒ
收иө·
(1)еӣ дёәдёүи§’еҪўABC,CDEеқҮдёәзӯүиҫ№дёүи§’еҪўпјҢжүҖд»ҘAC=BC,CD=CE;еӣ дёәB,C,DдёүзӮ№еңЁеҗҢдёҖжқЎзӣҙзәҝдёҠпјҢжүҖд»Ҙи§’ACD=180еәҰ-и§’ACB=180-60=120еәҰпјҢеҗҢзҗҶи§’BCE=180еәҰ-и§’ECD=120еәҰпјҢеҚіи§’ACD=и§’BCE.еӣ жӯӨдёүи§’еҪўACDе…ЁзӯүдәҺдёүи§’еҪўBCE,д»ҺиҖҢAD=BE.
(2)з”ұ(1)йўҳпјҢдёүи§’еҪўACDе…ЁзӯүдәҺдёүи§’еҪўBCE,жүҖд»Ҙи§’CAG=и§’CBE.еӣ жӯӨеңЁдёүи§’еҪўCBFдёҺдёүи§’еҪўCAG...
е…ЁйғЁеұ•ејҖ
(1)еӣ дёәдёүи§’еҪўABC,CDEеқҮдёәзӯүиҫ№дёүи§’еҪўпјҢжүҖд»ҘAC=BC,CD=CE;еӣ дёәB,C,DдёүзӮ№еңЁеҗҢдёҖжқЎзӣҙзәҝдёҠпјҢжүҖд»Ҙи§’ACD=180еәҰ-и§’ACB=180-60=120еәҰпјҢеҗҢзҗҶи§’BCE=180еәҰ-и§’ECD=120еәҰпјҢеҚіи§’ACD=и§’BCE.еӣ жӯӨдёүи§’еҪўACDе…ЁзӯүдәҺдёүи§’еҪўBCE,д»ҺиҖҢAD=BE.
(2)з”ұ(1)йўҳпјҢдёүи§’еҪўACDе…ЁзӯүдәҺдёүи§’еҪўBCE,жүҖд»Ҙи§’CAG=и§’CBE.еӣ жӯӨеңЁдёүи§’еҪўCBFдёҺдёүи§’еҪўCAGдёӯпјҢз”ұдәҺ и§’BCF=и§’ACG=60еәҰпјҢи§’CBF=и§’CAG,д»ҘеҸҠAC=BC,жүҖд»Ҙдёүи§’еҪўCBFе…ЁзӯүдәҺдёүи§’еҪўCAG,еӣ жӯӨCF=CG. еҸҲеӣ дёәи§’FCG=60еәҰпјҢжүҖд»Ҙдёүи§’еҪўCFGжҳҜжңүдёҖдёӘеҶ…и§’дёә60еәҰзҡ„зӯүи…°дёүи§’еҪўпјҢеӣ жӯӨеҝ…дёәзӯүиҫ№дёүи§’еҪўгҖӮ
(3)еӣ дёәCMдёәдёүи§’еҪўBCEдёӯиҫ№BEдёҠзҡ„дёӯзәҝпјҢCNдёәдёүи§’еҪўACDдёӯиҫ№ADдёҠзҡ„дёӯзәҝпјҢиҖҢе…Ёзӯүдёүи§’еҪўеҜ№еә”иҫ№дёҠзҡ„дёӯзәҝд№ҹзӣёзӯүпјҢжүҖд»Ҙжңү CM=CN.
иҝҷж ·еңЁдёүи§’еҪўANCдёҺдёүи§’еҪўBMCдёӯпјҢAN=1/2AD=1/2BE=BM,NC=MC,AC=BC,жүҖд»Ҙдёүи§’еҪўANCе…ЁзӯүдәҺдёүи§’еҪўBMCпјҢеӣ жӯӨи§’ACN=и§’BCM,д»ҺиҖҢи§’MCN=и§’ACM+и§’ACN=и§’ACM+и§’BCM=и§’ACB=60еәҰпјҢеҚіи§’MCN=60еәҰгҖӮеӣ жӯӨдёүи§’еҪўCMNд№ҹжҳҜжңүдёҖдёӘи§’дёә60еәҰзҡ„зӯүи…°дёүи§’еҪўпјҢд»ҺиҖҢдёәзӯүиҫ№дёүи§’еҪўгҖӮ
收иө·
е·Із»Ҹжңүдәәзӯ”дәҶпјҢиҖҢдё”жҜ”жҲ‘зҡ„ж–№жі•еҘҪпјҢе°ұдёҚеҶҷеҮәжқҘдёўдәәдәҶгҖӮ
1
и§’ACB=и§’DCE=60еәҰ и§’ACE=и§’ACE жүҖд»Ҙи§’ACD=и§’BCE
еҸҲеӣ дёәEC=DC AC=BC жүҖд»Ҙдёүи§’еҪўACDе…Ёзӯүдёүи§’еҪўBCE
жүҖд»ҘAD=BE
2
еӣ дёәдёүи§’еҪўACDе…Ёзӯүдёүи§’еҪўBCE
жүҖд»Ҙи§’FCE=и§’GDC еҶҚеӣ дёәCE=CD и§’FCE=и§’GCD=60В°
жүҖд»Ҙдёүи§’еҪўFCEе…Ёзӯү=дёүи§’еҪўGDC
еӣ дёәCG=FC жүҖд»Ҙи§’FC...
е…ЁйғЁеұ•ејҖ
1
и§’ACB=и§’DCE=60еәҰ и§’ACE=и§’ACE жүҖд»Ҙи§’ACD=и§’BCE
еҸҲеӣ дёәEC=DC AC=BC жүҖд»Ҙдёүи§’еҪўACDе…Ёзӯүдёүи§’еҪўBCE
жүҖд»ҘAD=BE
2
еӣ дёәдёүи§’еҪўACDе…Ёзӯүдёүи§’еҪўBCE
жүҖд»Ҙи§’FCE=и§’GDC еҶҚеӣ дёәCE=CD и§’FCE=и§’GCD=60В°
жүҖд»Ҙдёүи§’еҪўFCEе…Ёзӯү=дёүи§’еҪўGDC
еӣ дёәCG=FC жүҖд»Ҙи§’FCG=60В°
жүҖд»Ҙ в–іCFGжҳҜзӯүиҫ№дёүиҫ№еҪў
3
в–іACDе…ЁзӯүдәҺв–іBCE
д»ҺиҖҢ и§’CEB=и§’ADC BE=AD
жңү AM=MD=EN=NB
EN=DM и§’CEB=и§’ADC CD=CE
в–іCDNе…ЁзӯүдәҺв–іCEM
CM=CN
и§’DCN=и§’ECM
NCM=MCE+NCE=DCN+NCE=60
д»ҺиҖҢдёүи§’еҪўCMNдёәзӯүиҫ№дёүи§’еҪў
收иө·