еҰӮеӣҫ,ADжҳҜRtв–іABCзҡ„ж–ңиҫ№дёҠзҡ„й«ҳ,PжҳҜADзҡ„дёӯзӮ№,иҝһз»“BP并延й•ҝдәӨACдёҺE.е·ІзҹҘAC:AB=K,жұӮAB:EC
жқҘжәҗпјҡеӯҰз”ҹдҪңдёҡеё®еҠ©зҪ‘ зј–иҫ‘пјҡдҪңдёҡеё® ж—¶й—ҙпјҡ2024/08/27 20:40:34
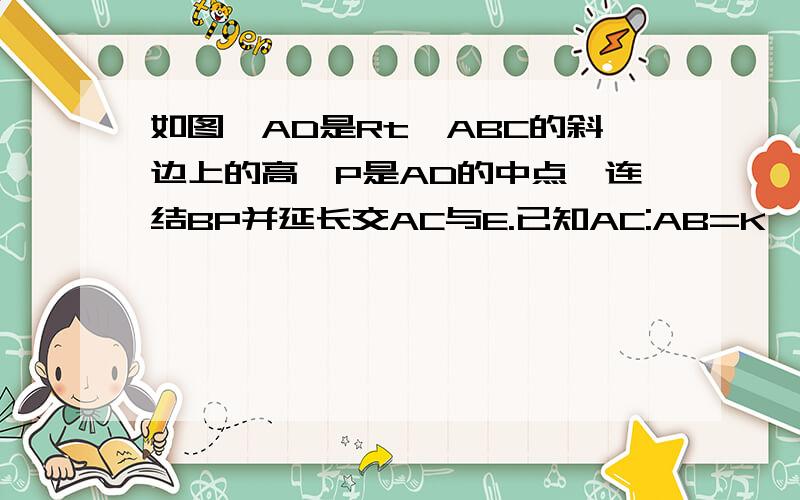
еҰӮеӣҫ,ADжҳҜRtв–іABCзҡ„ж–ңиҫ№дёҠзҡ„й«ҳ,PжҳҜADзҡ„дёӯзӮ№,иҝһз»“BP并延й•ҝдәӨACдёҺE.е·ІзҹҘAC:AB=K,жұӮAB:EC
еҰӮеӣҫ,ADжҳҜRtв–іABCзҡ„ж–ңиҫ№дёҠзҡ„й«ҳ,PжҳҜADзҡ„дёӯзӮ№,иҝһз»“BP并延й•ҝдәӨACдёҺE.е·ІзҹҘAC:AB=K,жұӮAB:EC

еҰӮеӣҫ,ADжҳҜRtв–іABCзҡ„ж–ңиҫ№дёҠзҡ„й«ҳ,PжҳҜADзҡ„дёӯзӮ№,иҝһз»“BP并延й•ҝдәӨACдёҺE.е·ІзҹҘAC:AB=K,жұӮAB:EC
еҫҲжҳҺжҳҫRtв–іADCвҲҪRtв–іBDAвҲҪRtв–іBAC
и®ҫBD=a,еҲҷAD=ka,еҲҷCD=k^2*a,еҲҷBC=(k^2+1)a
延й•ҝBE,并дҪңAF//BCдәӨBE延й•ҝзәҝдәҺF
вҲҙв–іAEFвҲҪв–іCEB,еҚіAFпјҡBC=AE:CE
вҲөPжҳҜADдёӯзӮ№,еҚіAP=DP,еҸҲAE//BC
вҲҙв–іAFPвүҢв–іDBP,еҲҷBD=AF=a
вҲҙAFпјҡBC=AE:CE
aпјҡ(k^2+1)a=AE:CE
AE:CE=1/(k^2+1)
вҲҙCEпјҡAC=(k^2+1)/(k^2+2пјү
вҲөAC:AB=k,еҚіAB:AC=1/k,
вҲҙAB:EC=1/k*[(k^2+1)/(k^2+2пјү]=(k^2+1)/(k^3+2k)