如图,∠MAN=60°,点B在射线AM上,AB=4.P为直线AN上一动点,以BP为边作等边三角形BPQ(点B.P.Q按顺时针排列),O是△BPQ的外心.1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上2)当点P在射线AN上
来源:学生作业帮助网 编辑:作业帮 时间:2024/11/16 10:15:37
如图,∠MAN=60°,点B在射线AM上,AB=4.P为直线AN上一动点,以BP为边作等边三角形BPQ(点B.P.Q按顺时针排列),O是△BPQ的外心.1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上2)当点P在射线AN上
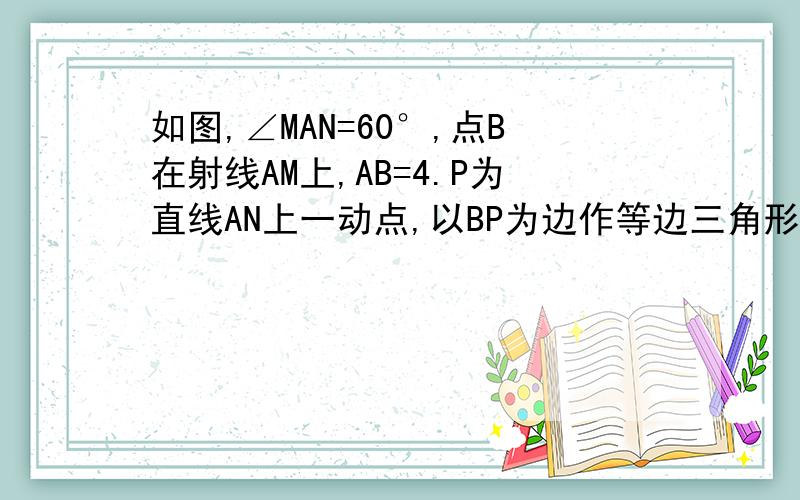
如图,∠MAN=60°,点B在射线AM上,AB=4.P为直线AN上一动点,以BP为边作等边三角形BPQ(点B.P.Q按顺时针排列),O是△BPQ的外心.
1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上
2)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=X,AC·AO=Y,求Y与X之间的函数关系式,并写出函数的定义域.
3)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离
一步一步写,有的同学p143
如图,∠MAN=60°,点B在射线AM上,AB=4.P为直线AN上一动点,以BP为边作等边三角形BPQ(点B.P.Q按顺时针排列),O是△BPQ的外心.1)当点P在射线AN上运动时,求证:点O在∠MAN的平分线上2)当点P在射线AN上
立达的right?
(1)证明:如图1,连接OB,OP,因为O是等边三角形BPQ的外心,所以,OB=OP.
圆心角∠BOP=360º/3=120º.
当OB不垂直于AM时,作OH⊥AM,OT⊥AN,垂足分别为H,T.
由∠HOT+∠A+∠AHO+∠ATO=360º,且∠A=60º,∠AHO=∠ATO=90º,
所以,∠HOT=120º.所以,∠BOH=∠POT.
Rt△BOH≌Rt△POT. 所以,OH=OT.
所以,点O在∠MAN的平分线上.
当OB⊥AM时, ∠APO=∠360º-∠A-∠BOP-∠OBA=90º.
即OP⊥AN.
所以,点O在∠MAN的平分线上.
综上所述,当点P在射线AN上运动时,点O在∠MAN的平分线上.
(2)解: 如图2,因为AO平分∠MAN,且∠MAN=60º,所以,∠BAO=∠PAO=30º.
由(1)知,OB=OP,∠BOP=120º,所以,∠CBO=30º,所以,∠CBO=∠PAC.
∠BCO=∠PCA,所以,∠AOB=∠APC.
所以,△ABO∽△ACP.
所以,AB/AC=AO/AP.所以,AC×AO=AB×AP.y=4x.
定义域为:x>0.
(3)解: ①如图3,当BP与圆I相切时,AO=2
